The coefficient of thermal expansion, often abbreviated CTE, provides a measure of how much a material expands or shrinks when heated or cooled. This is an important consideration for any material or product that will be exposed to extreme temperatures or temperature fluctuations. A material’s expansion or contraction could lead to critical errors in function and should be accounted for in any application. Learning how to calculate CTE is the first step to understanding its impact.
CTE units are expressed in strain per degree temperature. The equation for calculating the change in length (ΔL) of a component of length (L) due to a change in temperature (ΔͲ) is ΔL = L · α · ΔͲ. Rearranging, since the change in length divided by the original length is strain, thermal strain can be calculated as:
![]()
Strictly speaking, the coefficient of thermal expansion described above deals with expansion in one direction only. Therefore, sometimes you will see this written as the coefficient of linear thermal expansion. The coefficient of area expansion and the coefficient of volume expansion describe change in area per degree temperature rise and the change in volume per degree temperature rise, respectively. For isotropic materials, these values are respectively twice and three times the linear coefficient of thermal expansion:
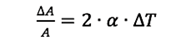
Again, it is important to note that this is for isostropic (non-directional) solid materials only, which means that their properties are the same in all directions. However, the value reported on solid material’s data sheet will almost always be the linear expansion coefficient, unless otherwise noted. (There may be more than one value reported, particularly for composite materials where the rate of expansion may be different in different directions.)
Thermal strain expands in all three directions vs. mechanical strain which expands in one direction and contracts in the other two. A thermal strain of 20% would make a part 20% longer, thicker and wider. A mechanical strain of 20% would make a part 20% longer, but 6% narrower and thinner, assuming a Poisson’s ratio of 0.3 (typical for most metals).
Like many other properties, the thermal expansion coefficient is not a constant, but instead is a function of temperature, as shown in Figure 1. Therefore, to accurately determine the thermal expansion and thermal strain, you will need to know not only the change in temperature, but what the starting temperature and ending temperature actually are, so you can use the proper value for CTE.
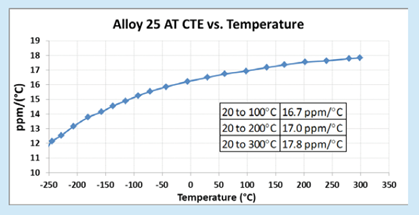
Figure 1. Two Different Methods of Presenting Thermal Expansion Data.
You could plot the curve of instantaneous CTE vs. temperature, as shown graphically above. Essentially, this is a plot of the instantaneous slope of the thermal strain vs. temperature curve. The other means would be to present a table of linear expansion rates to be used in a particular range of temperatures.
An example of a practical application of CTE is that you can use known expansion vs. temperature behavior to construct a simple temperature gauge. Bimetallic sensors and switches make use of two materials with different thermal expansion rates bonded together. Since the two materials expand at different rates, the composite will curve toward the shorter (less expanded or more contracted side), which is useful for temperature gauges or to simply activate or deactivate an electric circuit when the temperature goes beyond certain limits. There are also alloys that are specially designed to have low thermal expansion coefficients. The most well-known of these low expansion alloys is FeNi36, also known by the tradename Invar®. (The current holder of this trademark is Aperam SA.) Near room temperature, this alloy has a CTE an order of magnitude lower than most metals, as shown in Table 1.
Other alloys have CTEs that are matched to other materials. For example, Alloy 42 (FeNi42) and the FeNi29Co17 alloy known as Kovar® (currently a trademark of CRS Holdings, Inc.) have thermal expansion coefficients that are matched to glass and ceramic materials. This makes them ideal for hermetically sealed processor or sensor packages, where it is important to remain sealed no matter how hot or cold the package gets. A differential thermal expansion could easily break such a seal, so CTE-matched alloys are usually used here.
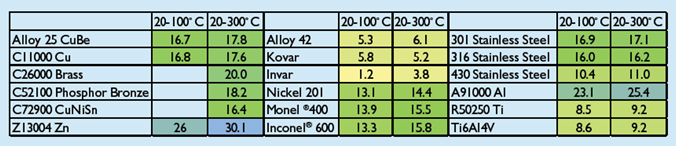
Table 1. Coefficient of Thermal Expansion for Various Metals at 20-300˚C.
The above are in ppm/˚C. Monel® and Inconel® are registered trademarks of Special Metals Corporation. Get more details about Alloy 25, or learn about our other high-strength, copper-beryllium alloys here.
Under certain conditions, the coefficient of thermal expansion can be negative. For example, between 0°C and 4°C, water will expand as it cools and contract as it warms. There are certain other compounds that show negative thermal expansion coefficients over wide temperature ranges such as cubic zirconium tungstenate (ZrW2O8). There are also some artificially constructed metamaterials that show this behavior as well.
The thermal expansion coefficient provides useful information for several applications, although it is another property that varies with temperature. To do meaningful calculations, you will need to know the coefficient that is appropriate for the temperature range you are working in. Contact us and we will be happy to assist with finding the right material for your application.
Thanks for joining us for another edition of In Our Element. For ongoing industry updates, connect with us on LinkedIn.