In our increasingly connected world, it’s not enough to design electronic components just to make good electrical contact. Most devices in modern life contain an electronic component, so they must also be constructed to withstand the high forces created by colliding with solid objects. Suddenly applied loads (called “shock loads”) place a large amount of stress on electronic components in a very short time. This may result in sudden failure of the device or component due to the deformation or fracture of connectors and interconnection devices. Making the consumer devices smaller and lighter helps lower the force of impact but designing the individual parts to absorb more of the impact energy themselves can be key to preventing malfunctions.
The conditions of random shocks and vibrations are usually simulated in a laboratory by drop tests. To understand those tests and the viability of electronic components to be used in production, it is important to learn more about impact resistance. Please note that this is not the same as impact strength or toughness as a material property - this article will describe the resistance of electronic devices to shock and impact loads.
Since there is elasticity in all collisions, a drop test can be modeled by the impact of a weight with a spring. A spring that has a weight (W in the figures below) resting on it will be deflected a certain amount (dST) from its free height (Figure 1).

Figure 1. Static Deflection
The force on the spring would be equal to the weight of the object. However, if the object were dropped onto the spring from a given height (h), the spring would be deflected much farther (Figure 2). The force (F) on the spring would be equal to the weight of the object multiplied by an impact factor (Figure 3).
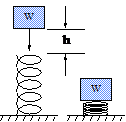
Figure 2. Impact Deflection
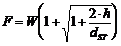
Figure 3. Impact Force
It is important to note that if an object is held at the top of an uncompressed spring and then released, the force generated would be equal to twice the weight of the object. For an object dropped from a height (as in most drops), the force experienced would exceed twice the weight of the object.
The kinetic energy of a freely falling object that started from rest is equal to the weight of the object multiplied by the distance it has fallen (assuming no air resistance). If the object did not start at rest, i.e., being thrown, it will probably have even greater kinetic energy at the time of impact. When the object hits the ground, all energy must be conserved. Some of it will be converted to sound, some will be converted into upward motion as the object bounces, and the rest will go into deforming the device and its individual components.
When an object is dropped and the deformation is small enough, the components will elastically return to their original shape. When there is too much energy to absorb, components will permanently deform and may even break or be damaged beyond repair. This is why it’s important to design components to absorb as much impact energy as possible.
First, you must know how to find the amount of energy a component can absorb. The formula for the amount of energy absorbed by a rod (such as a connecting pin) suddenly exposed to tension or compression by an impact is displayed in Figure 4. To determine the amount of energy that can be absorbed without permanent set, substitute the yield strength for the stress term in the equation.
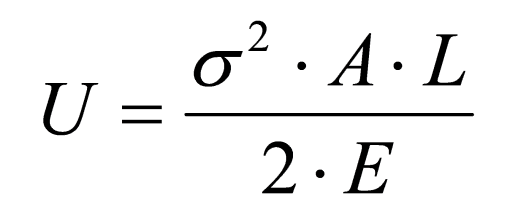
Figure 4: Impact Energy
In Figure 4 above, U is the energy absorbed by the rod, σ is the stress created by the deformation, A is the cross-sectional area, L is the length, and E is the elastic modulus of the material.
In practice, larger contacts will have more energy absorbing capacity than smaller contacts. However, the telecommunications and computer industries are trending towards reduced sizes. This lessens the amount of energy these devices can safely absorb, making it increasingly important to choose materials with properties that can offset these losses.
By using a material with a different elastic modulus, it is possible to slightly increase the amount of impact energy that the component can absorb. The elastic moduli of copper alloys vary from 16,000,000 psi to 20,000,000 psi (110 to 138 GPa), a difference of 25%. The alloy with the lowest modulus will only have 25% more energy absorbing capacity than the alloy with the highest modulus. If the volume of the object has been reduced 25% or more, this does not create a benefit.
The value of yield strength has the greatest impact on the amount of energy absorbed without permanent deformation. The yield strengths of copper alloys vary from 50,000 psi to 205,000 psi (340 to 1415 MPa). The alloy with the highest strength will have almost sixteen times as much energy absorbing capacity than the lowest strength alloy. A 10% increase in yield strength will create a 21% increase in impact strength. A 20% increase in yield strength will create a 44% increase in impact strength. Clearly, it is vital to use a material with as high a yield strength as possible in order to provide devices that can withstand the forces of impact.
This discussion has been about absorbing shock loads without permanent set. To consider the amount of energy absorbed without fracture (fracture toughness or impact strength) then the total elongation and the full stress-strain behavior of the material comes into play as well.
Find out how our materials provide superior impact resistance to consumer electronics products on our website.
Thanks for joining us for another edition of In Our Element. For ongoing industry updates, connect with us on LinkedIn.